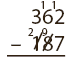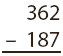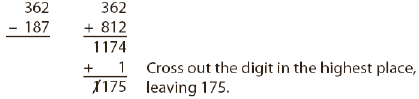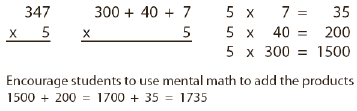There's More Than One Way to Get to St. George!

Summary

Students will explore alternative ways to do the four operations.

Materials

• Map of Utah

Addition...It's Magic!

• Copy of the painting "Melancholia" by Albrecht Durer
• Ben Franklin and the Magic Squares
  

Subtraction Around the World

• Globe
• Pictures of cities and/or people from Europe, Russia, and China
• Charts with three different algorithms

Multiplication...A Great Invention!

• 1/2” graph paper
• Globe—Show location of different countries discussed in Background Information
• Picture of Fibonacci
• Chart of Roman numerals
• Piece of garden lattice
• Red and blue colored pencils
• Dice

Division...Why Does It Take So Long?

• Counters
• Graph paper
• Multiplication charts
• Number lines
• A Remainder of One

Additional Resources

Books

1. Teaching Arithmetic: Lessons for First Grade, by Stephanie Sheffield; ISBN 0941355349
2. Ben Franklin and the Magic Squares, by Frank Murphy; ISBN 0375806210
3. Math Homework that Counts, Grades 4-6, by Annette Raphel; ISBN 0-941355-27-6
4. A Remainder of One, by Elinor Pinczes; ISBN 0-618-25077-8

Article

• Magic Squares, by Ivars Peterson, in Muse, Nov/Dec 2003.

Organization

• National Council of Teachers of Mathematics, http://illuminations.nctm.org

Miscellaneous

• Dixie Blackinton, Weber State University
  Diane Pugmire, Weber State University
  Sculpey® III Basic Color Set, (available from Dick Blick Art Materials, http://www.dickblick.com or (800) 723-2787); Item #33218-1019

Background for Teachers

In Lessons for First Grade, 2000, Stephanie Sheffield quotes a first grade teacher:

“If you followed the rules and put the numbers in the right places, you got the answer right. To be truthful, arithmetic never made much sense to me. In fact, it never occurred to me that the facts I learned and the algorithms I performed were supposed to make sense.”

As both students and teachers, the majority of us have bought into the theory that there is only one right way to do math, and that was to simply memorize the algorithm shown to us. This is not true, in fact there are many different ways to DO math as long as we reach the correct answer. This lesson explores teaching students alternative ways to do the four operations, with the underlying message being that there are many ways to get to the correct answer, and that as long as you understand the meaning of the operation and how it works, you can use the strategy that best suits you and the problem you are working on. It is critical for students to develop adequate conceptual understanding and computational fluency so they are able to accurately complete problems using a variety of methods. Prior knowledge of the meanings of the four operations and mastery of the basic facts is essential for the success of this lesson.

Intended Learning Outcomes

1. Demonstrate a positive learning attitude toward mathematics.
2. Become mathematical problem solvers.
3. Reason mathematically.

Instructional Procedures

Invitation to Learn

1. Pass out a Map of Utah to each student.
2. Put students into small groups and ask them to find a way to get to St. George from the state capitol. Encourage them to try and find a route they think will be unique.

Journaling Activity—Have participants work in groups to find several different routes and record them in their journals.

3. Have each group choose a reporter and share their route with the class.
4. Discuss how we all ended up in the correct place, even though we didn’t all get there exactly the same way. Explain that this is true for many areas of our lives and amazingly, it is also true for math. Ask how many of them think that there is only one right way to do math. Have them do a subtraction problem requiring regrouping and see if they all do it the same way. Is it accurate to say that they could have done that problem several different ways as long as they did one really important thing? The answer is yes, there are lots of ways to do that problem, but what is that one critical thing you must all do the same? Get the correct answer! So, just as there are many ways to get to St. George, there are many ways to do math as long as we end up with the correct answer.

Instructional Procedures
This lesson includes an activity for each of the four operations. Teach each part as you work on that specific operation. Remind students of the big idea, “there is more than one way to get to St. George and to do math” as you present each lesson.

Addition...It’s Magic!
To reinforce conceptual understanding, teach/review expanded form addition, which visually shows what is happening when you regroup in addition and encourages students to use their mental math skills.

This activity provides fourth graders the opportunity to practice addition in a way that engages and interests them. Adapted from Magic Squares, by Ivars Peterson in Muse, Nov/Dec 2003.

1. Present background information on magic squares. Do you have a lucky number? In ancient China, people believed that a special arrangement of nine numbers in a square was especially lucky. They engraved this pattern on stones and medallions worn as charms to ward off evil or bring good fortune. They thought it was lucky because of a legend that told of a divine turtle that appeared in a Chinese river over 4,000 years ago. This turtle had a magic square on its back. Since then, many cultures have had their own version of magic squares and the influence they were supposed to have in people’s lives.
2. Many well known people have also been fascinated with magic squares. Show “Melancholia” by the German artist Albrecht Durer and see if the class can find a magic square in it.
3. Benjamin Franklin used to make up magic squares when he got bored listening to political speeches. Share the book, Ben Franklin and the Magic Squares.
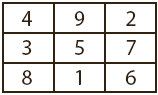
4. So what are magic squares and how do they work? Let’s find out. Show this magic square on the board or overhead.

Use addition to see if you can find the magic in this square. When you add the numbers in the rows, columns, and diagonals you get the same sum...15. That is the magic constant. In order to be a true magic square, you must always get the magic constant.

5. Here are three more examples. Two of them are true magic squares, and one is not. Use your addition skills to discover which square is the imposter.

Journaling Activity—Have students work in groups to create a magic square of their own. Share results with whole group so they have several more examples.

Subtraction Around the World
The following is an excerpt from Relearning to Teach Arithmetic by Susan Jo Russell:

“When all computation was done by hand, it was important to reduce the computation process to the smallest number of steps. Imagine what it was like to keep records for a small business not only before the advent of calculators and computers, but before even adding machines were available. People who needed to do many calculations again and again wanted as many pencil and paper shortcuts as possible.

Which of these paper and pencil shortcuts were chosen to be taught in public schools is, in part, a matter of historical accident. At other times in our history and in other countries, the schools have taught algorithms different from those considered standard in American education. Although many of us assume that what we’ve been taught must be the best algorithms, this is not necessarily true from a mathematical point of view and certainly not from a pedagogical one.”

Many students, parents, and teachers are astounded to learn that not everyone on earth subtracts exactly as we do. This lesson introduces a few of the different methods of subtraction used around the world. Adequate conceptual understanding of the meaning and use of the subtraction process is an important prerequisite skill in order for this lesson to work. This lesson is ideally suited to those students who are able to accurately compute with the standard subtraction algorithm and are ready to handle the challenge of learning some new and different methods.

1. Invite several students to come to the front of the room. Spin the globe and have them close their eyes and put their fingers anywhere on the globe when it stops. Point out the places they have picked and explain that if we were able to visit a math class in those areas we might be astounded to see that 10-year old students there are doing math differently than we are.
2. Show the pictures of each area and its location on the globe as you briefly introduce each type of subtraction. In Europe, students can subtract numbers without ever having to regroup. In Russia, students subtract from left to right (the opposite of us). In China and other Oriental countries, they don’t subtract at all, they change the problems into addition! Today we are going to see examples of problems using the methods from these three countries. You will most likely not be able to accurately use any of these after just one exposure to them. But, if you think a method looks interesting, you are encouraged to practice it on your own. Who knows...you just might find an alternative method that works better for you than the standard algorithm you are used to!
3. Introduce European Method

Start in the ones column. You can’t subtract 7 from 2, so make the 2 a 12. You also have to add one to the bottom number in the tens column which is 8, and make it a 9. Now you can subtract 7 from 12 and write the answer of 5 in the ones place in the answer. Now look at the tens column. You can’t subtract 9 from 6, so make the 6 a 16. You also have to make the 1 in the hundreds column into a 2. Now subtract 9 from 16 and the answer 7 in the tens place. Now look at the hundreds column, you can subtract 2 from 3 so write the answer of 1 in the hundreds place.

Journaling Activity—Write an explanation of how and why you think this method works.

4. Introduce Russian Method

With this method, you start on the left in the hundreds column. 3 subtract 1 is 2, but before you write down the 2, you must look at the tens column and see if there is going to be a problem (subtrahend larger than minuend). There is, so you write down a 1 instead of a 2. Move to the tens column. You can’t subtract 8 from 6 so you do the following procedure: decide how much more you need to add to 8 to make it 10....it’s 2. So add 2 to the 6 to make it 8. But, before you write that down in the tens place, look at the ones column to see if there is going to be a problem. There is, so instead of writing down the 8, reduce it by 1 and write a 7. Now move to the ones column. You can’t subtract 7 from 2, so do the following procedure: decide how much more you need to add to 7 to make it a 10...it’s 3. Add 3 to the 2, you get 5 so write 5 in the ones place.

Journaling Activity—Try a problem with 0 using this method and see what happens. Can you explain what you would need to do differently and why?

5. Introduce the Oriental strategy—Change subtraction to addition!

Change the subtraction problem into an addition problem by replacing each digit in the subtrahend with difference between that number and 9. For example: The difference between 1 and 9 is 8, so you write 8 in the hundreds place. The difference between 8 and 9 is 1, so you put 1 in the tens place. The difference between 7 and 9 is 2 so you put 2 in the ones place. Now add. When you finish, drop the 1 in the largest place and add 1 to the ones place.

Journaling Activity—Which, if any, of these methods do you think would be a good alternative to our standard algorithm and why?

Multiplication...A Great Invention!

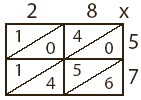
1. Share information on the background of lattice multiplication with class. Explain terms and ideas as needed and/or explain in your own words. The lattice method of multiplication appeared in the first printed arithmetic book, printed in Italy in 1478. Lattice multiplication and variations of the standard long 2-digit multiplication algorithm used today were introduced in Europe by Fibonacci (show picture). He was an Italian whose father was a diplomat. He traveled widely with him and was educated in North Africa where he learned the Hindu-Arabic number system (the system we use today) from a Moorish teacher. He was convinced that this number system was superior to the systems used in Europe and when he returned to Italy he wrote a book called Liber Abacci explaining the new system. The book became very influential in convincing Europeans to switch to the Hindu Arabic number system from the old Roman Numeral System (show chart) they were using. Before this number system was introduced, multiplication was very difficult and could only be done by a few people using counters. The Hindu-Arabic number system was much better suited to multiplication than the old Roman Numeral System and made multiplying fairly simple and accessible to many more people. This allowed people to keep better track of the increasingly large amounts of products and goods they were dealing with.
2. Show the lattice to students. Tell them that this is the same arrangement we use to do lattice multiplication and it might help them remember it better.
3. Pass out the graph paper and have students draw their boxes and diagonals. If this is difficult, make lattice boxes on the computer and run them off.
4. Demonstrate the lattice multiplication process. Use the red pencil to record products and the blue to record sums. 28 x 57 = _____

Multiply each partial product and record it as shown above, putting one digit in each section of the box.

5 x 8 = 40
5 x 2 = 10
7 x 8 = 56
7 x 2 = 14

5. Add the numbers on the diagonals. It helps to extend the diagonal lines just slightly, and put a + sign outside the bottom left hand corner of the box. You must start on the bottom right so you can carry to the next diagonal if necessary. Record your sums at the bottom of each diagonal.

Start with the top left number and write them down, 1596. Your answer is 1,596.

6. Now do 65 x 29, which requires regrouping.

Division...Why Does It Take So Long?
This lesson introduces a “short division” process for students who have the ability to use a “shortcut” when dividing 2 and 3 digit dividends by 1 digit divisors. Students who have been taught both methods can choose which strategy to use on which problem. You will see students alternate between the two processes depending on which works better for them on that problem. We experimented with different classes to see if learning short division before or after long division was more effective. For the majority of students, it worked best to teach long division first, then they understood and appreciated the short division process more.

The rationale behind this method is this: “From first grade, students have learned to add and subtract from right to left starting with the ones place. The long division form attempts to teach students to work from left to right, which goes counter to all previous learning. Also students must master a series of steps (divide, multiply, subtract, bring down, remainder) which uses several difficult math concepts and is often confusing, especially the bring down step. Short division eliminates that step and the only step the students use is to divide the number and find how many are left over.”

1. Share Remainder of One to review concept of “how many left over.”
2. Teach short division method as follows, using counters to demonstrate.

Write problem in division box format, spacing numbers slightly apart.

Ask:	How many groups of 3 are there in 7? xxx xxx x (2) Write the 2 on top in the quotient place.
Ask:	How many were left over? (1) Place the 1 slightly below and to the left of the next digit—3. Explain that this is just like the carrying they did in addition and multiplication, and the 3 is now a 13.
Ask:	How many groups of 3 are there in 13? xxx xxx xxx xxx x (4) Write the 4 on top in the quotient place.
Ask:	Were there any left over? (Yes—1.) Is there another digit in the dividend? (No.) Then the 1 is a remainder. Write it as R1 in the quotient place.
Check:	Your quotient was 24 R1. Check with x and +. 24 x 3 = 72 + 1 = 73

Extensions

• Advanced learners may enjoy experimenting with inventing their own methods.
• Struggling learners can be exposed to the different methods, but may be better served by using only one method.
• Students make their own Chinese magic square medallions using Sculpey® III oven bake clay. Have students shape Sculpey III into medallion shapes, carve a magic square onto it, make a hole for ribbon, bake following package directions, then paint and hang them with ribbon.
  Materials
  • Sculpey III
  • Ribbon
  • Acrylic paints
    
• Do magic squares online at scienceforkids.org MatheMUSEments section
• Encourage advanced learners to continue making their own magic squares. Challenge them to try 4 x 4 squares and even larger. Ben Franklin is famous for an 8 x 8 one!
• Advanced learners might enjoy looking up more information about Fibonacci and some of the other math concepts he is credited with. They could also look up other great mathematicians and learn more about their discoveries and methods.
  
• Teach both the lattice and standard algorithm. When students miss a problem using one method, have them rework it using the other method.
• For students who are still struggling with understanding the meaning of multiplication try playing the game "Circles and Stars." This reinforces the understanding of multiplication being repeated addition and its commutative property. Students work in partners. Partner A rolls two dice. S/he chooses one die to represent the number of circles s/he will draw, and the other to represent how many stars s/he will draw in each circle. Partner B repeats the activity. The game continues for seven rounds. They total the stars at the end using multiplication and the player with the highest total wins.
• Partial product multiplication is also helpful to develop students' conceptual understanding of the multiplication process.

Assessment Plan

• Observe students and/or have them write about their attitudes toward math to assess whether having the freedom to use different methods has helped them develop more positive attitudes.
• Collect samples of student work to assess their progress.
• Do a survey of which methods students prefer and make a graph to show data. Discuss pros and cons of each method.
• Use formal written assessments using problems appropriate for each operation.

Bibliography

Research Basis

Russell, S. J. (1999). Developing Fluency—Relearning to Teach Arithmetic Study Guide Dale Seymour Publications

This text explains the importance of helping students develop a sound understanding of how and why the standard algorithms work, and provides alternative methods for doing the operations.

Herrera, T. & Myers, F.A. (2000). The Mystery of Mastery: A Rationale ENC Online

This text provides ideas and lesson plans for developing conceptual understanding.