Writing Variable Expressions For Physical Models, Patte
Summary
Write algebraic expression for models, patterns, and tables. Evaluate expressions for given values
Materials
Attachments
- TI-73's and Viewscreen or Presenter
- Algeblocks, Color Tiles, Centimeter Cubes or Linking Cubes
- Worksheets: Writing The Rule Game record, Building A Square Patio, Algeblocks Lab 1-3, 1- 4 (if available), Painting Towers, "Variable Expressions and Patterns in a Table"
- Journal page: Algebraic Expressions for Representing Patterns
Background for Teachers
Enduring Understanding (Big
Ideas):
Algebraic expressions can model
physical models and patterns
Essential Questions:
- Why are variables useful in describing patterns, physical models and tables?
- How can a model or a pattern be represented by a variable or a variable expression?
- When is substituting values used in the real world?
- How does the result change when the value of the variable is changed?
Skill Focus:
Write variable expressions for
physical models. Evaluate
algebraic expressions given values
for the variable.
Vocabulary Focus:
Variable, variable expression, algebraic expression,
substitute values
Ways to Gain/Maintain Attention (Primacy):
predicting, manipulatives, cooperative
learning, graphic organizer, writing, game
Instructional Procedures
Attachments
Starter:
- No calculators please: 1 ½ + ¾
- Which pair of numbers is relatively prime? Why?
3, 12 or 8, 15 - What is the Greatest Common Factor for 12 and 24?
Lesson Segment 1: Introduce vocabulary terms
Show this two-column comparison asking students to compare the expressions in the
left column to those in the right column. Expressions on the right contain a variable.
Operations and numbers are the same. One of the numbers in the numerical
expression has been replaced by a variable in the corresponding variable expression.
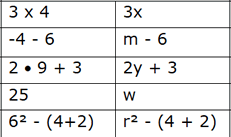 As students describe similarities and differences in
the expressions, introduce the vocabulary terms:
variable expression, algebraic expression and
variable. For each variable expression, a value
has replaced the variable in the corresponding
numerical expression. Show students how the
value can be replaced (substituted).
Q. If the variable on the right were replaced by
the value in its place on the left, would the result
of the variable expression be equal to the result of
the numerical expression? Why?
As students describe similarities and differences in
the expressions, introduce the vocabulary terms:
variable expression, algebraic expression and
variable. For each variable expression, a value
has replaced the variable in the corresponding
numerical expression. Show students how the
value can be replaced (substituted).
Q. If the variable on the right were replaced by
the value in its place on the left, would the result
of the variable expression be equal to the result of
the numerical expression? Why?
Lesson Segment 2: Why are variables useful in describing patterns? When is substituting values used in the real world? How does the result change when the value of the variable is changed?
Use Think-Team-Share where class members think for a few seconds, then talk with their team, then share with the class if selected.
Using this sequence: 25, 20, 15, 10, 5…
Q. What is the rule for this sequence? Subtract five each time.
Q. If X represents the one term you see in the sequence, what is an algebraic expression for finding the next term. n + -5 (All subtraction will be written using a related addition expression.)
Q. How can this algebraic expression, n + -5, help us find the next term in the sequence if the the term we see is -20? We can substitute -20 for the n because -20 is the term we know. -20 + -5 = -25
Q. Find the next term in the same sequence if each of the following last terms is the term you you are looking at.
- -15
- -300
- -1,000
Have students explain how they are finding the next term. Tell them, they have been substituting values for X. Have them write the algebraic expression n + -5 on their paper and show them how to write the symbolic expressions as they substitute each of the values given above.
Stand Up If: (Write these expressions on the overhead, and have student stand as you point to each to indicated which doesn't belong. Say, "Stand if this expression doesn't belong."
| 9m -- 1 | -3 + 4 | 5 -- p | X + 12 | 3w -- 7 |
Ask students how they identified the one that didn't belong. In the expression, -3 + 4, no value can be substituted for a variable because there is no variable. The value for - 3 is always -3. The value for 4 is always exactly 4.
All patterns and sequences can be modeled using operations in numerical or variable expressions.
Q. Think-Team-Share For example, in this sequence: 1, 2, 3, 4, 5, 6…, what operation is happen to each term to get the next term? We can write the rule for finding the next term using math symbols. So n + 1 would be the rule to help us find the next term.
Demonstrate using the graphing calculator as explain on the attached "Writing The Rule" activity. Then play "Writing The Rule". Instructions are attached.
Lesson Segment 2: How can a physical model be represented by a variable or an algebraic expression? When is substituting values used in the real world? How does the result change when the value of the variable is changed?
"Algebraic expressions can be used to represent physical models." Using Algeblocks pieces, tell the Candy Bar story as shown below having students sketch each of the situations, write algebraic expressions and substitute values as shown.
The Candy Bar Eating Contest
This ![]() represents exactly one unit. If I were talking about dollars, it would
represent exactly one dollar. If I were talking about boyfriends, it would represent
exactly one boyfriend. If I were talking about temperature, it would represent exactly
one degree. If I were talking about how many pencils I bought, it would represent
exactly one pencil. We'll call this piece 1.
represents exactly one unit. If I were talking about dollars, it would
represent exactly one dollar. If I were talking about boyfriends, it would represent
exactly one boyfriend. If I were talking about temperature, it would represent exactly
one degree. If I were talking about how many pencils I bought, it would represent
exactly one pencil. We'll call this piece 1.
This ![]() represents an undetermined value. When we are talking about an
undetermined value, we say words like, a few or many or some or several,
but we don't say an exact value like 3 or 7. We'll call this X.
I'm going to have you sketch these as I tell you about the Candy Bar Eating Contest.
(Student sketches and writing are indicated in color)
represents an undetermined value. When we are talking about an
undetermined value, we say words like, a few or many or some or several,
but we don't say an exact value like 3 or 7. We'll call this X.
I'm going to have you sketch these as I tell you about the Candy Bar Eating Contest.
(Student sketches and writing are indicated in color)
Four students were arguing about who could eat the most candy bars, so they decided to have a contest.
Amy said she could eat 3 candy bars. Let's sketch and label the number of candy bars Amy claims she can eat.
![]()
![]()
![]() 3 represents the number of candy bars for Amy.
3 represents the number of candy bars for Amy.
"Well", said Jen, "I can eat many more than you!"
Q. How would we represent many? It can't be an exact number.
![]() X represents the number of candy bars for Jen.
X represents the number of candy bars for Jen.
"That's nothing", said Parker, "I can eat twice as many candy bars as Jen can eat.
Q. How would you represent the number of candy bars Parker can eat?
![]()
![]() 2X represents the number of candy bars Parker can eat.
2X represents the number of candy bars Parker can eat.
Not wanting to be outdone, Sean brags that he can eat 4 more candy bars than Parker
can eat.
Q. How would you represent the number of candy bars Parker can eat?
2x + 4 represents the number of candy bars Sean can eat. |
||
Q. If the number of candy bars Jen can eat is 5, how many candy bars would each person have to eat? 3 for Amy, X = 5 for Jen, 2X or 2(5) = 10 for Parker, and 2X + 4 or 2(5) + 4 = 14 for Sean
You may want to use Algeblocks and the Lab 1-3 and Lab 1-4 worksheets to help students practice representing physical models.
Play Tic Tac Toe to Practice. Divide the class into two teams A and B. Have teams pick a number from 1-10 to determine who goes first. Give a problem from below. Give all students a chance to work with their teammates at their table to do the problem. Call on one person from Team A to explain the problem on their own (no coaching from team once you select the responder). If correct, the person comes to the board to put their X or O in the Tic Tic Toe game you have drawn. If the person is not correct, the question goes to a person you select from Team B to correct.
Give the next question. Give all students a chance to work with their teammates at their table to do the problem. Call on one person from Team B to explain (Yes, even if they corrected Team A on the last question. It is still their turn.) Continue the game until one team wins or there is a tie.
If this ![]() represents X units, and this
represents X units, and this ![]() is exactly one unit.
is exactly one unit.
- Sketch 2X + 2
- Sketch 4X+ 2
- Sketch 2X + 4
#4, 5, 6. If I give you the value of 6 for X, find the value for each algebraic expression above.
Write an algebraic expression for each sketch below.
Use Color Tiles to write variable expressions and substitute values as directed in "Building Square Patios" (attached). Tell students they have built the square patios before, but did not write variable expressions for the patterns. Now they will write variable expressions for the patterns. Remind them that the value of a variable can vary. Variable expressions: Added on is 2n -- 1, Perimeter is 4n, Area is n²
Lesson segment 3: How can a pattern in a table be represented by a variable expression? When is substituting values used in the real world? How does the result change when the value of the variable is changed?
Use centimeter or linking cubes to build the physical model and complete the table on the "Painting Towers" worksheet.
Variable expressions can describe the pattern or rule found in a table. Values from a table can be substituted in a variable expression. Work with the students to apply the variable expressions given on # 1-4 of the "Variable Expressions and Patterns in a Table" worksheet (attached). The follow the steps below for using a Ti-73 to build tables having the students find the variable expression that represents the relationship of y to x.
Writing and Evaluating Algebraic Expression Using A Table
To help students find patterns in a table and use those patterns to write an algebraic expression follow these steps:
- In
 type x + 1
type x + 1
- In
 select 0 for the table start number, 1 for the delta, and Auto
for the independent and dependent variables. Kids should not see these
first two steps.
select 0 for the table start number, 1 for the delta, and Auto
for the independent and dependent variables. Kids should not see these
first two steps.
- Press
 . Tell students some operation(s) has been performed on
the number in the first column to get the result in the second column.
Whatever that operation was, has been performed on each number in the
first column. That operation(s) can be called the rule. Ask them to look at
the numbers and find the rule. Have class members share their ideas.
Students may say, "one has been added to the number in the first column
to get the number in the second". Explain that if we call the number in the
first column "X", we could write math symbols to represent the rule.
Thus, x + 1 is the algebraic expression for the rule.
. Tell students some operation(s) has been performed on
the number in the first column to get the result in the second column.
Whatever that operation was, has been performed on each number in the
first column. That operation(s) can be called the rule. Ask them to look at
the numbers and find the rule. Have class members share their ideas.
Students may say, "one has been added to the number in the first column
to get the number in the second". Explain that if we call the number in the
first column "X", we could write math symbols to represent the rule.
Thus, x + 1 is the algebraic expression for the rule.
- Ask them to use the rule to tell what the value in the second column
would be if the number in the first column were 50, 7.5, -4, 2/5 etc.
Students should record the expression and values in # 5 on the "Variable
Expressions and Patterns in a Table" worksheet.
Repeat steps 1 -- 4 using 2x -- 1 (You may want to change table start to a negative integer or the delta to 0.5 to give them practice with numbers other than positive whole numbers.) Record in # 6 on the worksheet. - In
 type x -- 2
type x -- 2
- In
 select 0 for the table start number, 1 for the delta. This time
use Auto for the independent and Ask for the dependent variable. Kids
should not see these first two steps.
select 0 for the table start number, 1 for the delta. This time
use Auto for the independent and Ask for the dependent variable. Kids
should not see these first two steps.
- Press
 . In the Y column, press enter for a few of the values and
leave one or two values blank. Ask the students to find the rule, write an
algebraic expression for that rule and use that expression to find the
missing values in the second column. Have students record in # 7 on their
worksheet.
. In the Y column, press enter for a few of the values and
leave one or two values blank. Ask the students to find the rule, write an
algebraic expression for that rule and use that expression to find the
missing values in the second column. Have students record in # 7 on their
worksheet.
Repeat steps 5 -- 7. (You may want to change table start to a negative integer or change the delta to 0.5 to give them practice with numbers other than positive whole numbers.) Use 3.8 -- x. Record in # 8 on the worksheet.
Lesson Segment 4: Summarize
Have students work with partners to complete the journal page, "Algebraic Expressions
for Representing Patterns". Then pair partners with another pair to have them show
and share the examples they wrote on the page.
Assessment Plan
observation, performance task, journal
Bibliography
This lesson plan was created by Linda Bolin.
Updated: 02/05/2018


 UTAH EDUCATION NETWORK
UTAH EDUCATION NETWORK

 Justin
Justin Braxton
Braxton Dani
Dani Kayla
Kayla Katie
Katie Matthew
Matthew Rob
Rob Val
Val
