Finding Circumference and Area of a Circle
Main Core Tie
Mathematics Grade 7
Strand: GEOMETRY (7.G) Standard 7.G.4
Summary
Find circumference and area of a circle.
Materials
Attachments
- 5 cylindrical containers including a tennis ball canister
- Book "Sir Cumference and the First Round Table"
- Calculators
- Sir Cumference and the First Round Table Vocabulary
- Circumference Guess
- Counting The Area Of A Circle paper
- Circles Vocabulary
Background for Teachers
Enduring Understanding (Big Ideas):
Formulas can be used to find measurement of area and circumference
Essential Questions:
- What information is needed to find circumference of a circle? How can I find the circumference?
- What information is needed for finding area of a circle? How can I find the area for a circle?
Skill Focus:
Find circumference and area of a circle
Vocabulary Focus:
Diameter, radius, circumference, pi
Ways to Gain/Maintain Attention (Primacy):
Story, movement, sketching, visualizing, estimating, cooperative structure, movement
Instructional Procedures
Attachments
Starter:
Which in each pair has the greater perimeter? The greater area?

- Amy has 36 feet of fencing to make a dog run. She can make a 6 x 6 enclosure or a 4 x 9 enclosure. Which would be best for the dog run? Why do you think so?
Lesson Segment 1: What information is needed to find circumference of a circle?
Literature: Read "Sir Cumference and the First Round Table" (Cindy Neuschwander, 1997). As you come to shapes for each table, have the students sketch and label an example on the Math Journal page, Sir Cumference and the First Round Table Vocabulary. Especially focus on the words pertaining to the circle: circumference, diameter, radius.
Estimating: Circumference Guess
Helping Students Visualize Circumference
 To help your students visualize the relationship between the diameter and the circumference, select four cylindrical objects such as a glass, a film canister, a toilet paper roll, etc. A tennis ball canister with the three balls inside should be one of these objects. Have students number their paper 1-4 and write the name of each item. Tell them you will be having them decide which is greater, the circumference of the object or the height of the object. As you show them each object, they should write their guess for which is greater, either "circumference" or "height", next to the name of object. When they have written their guess for each object, show the length of the circumference by wrapping a measuring tape around the object. Then hold that length along the height so the students can compare the two lengths. They will be surprised when the circumference proves to be longer than the height of the object, because circumference is difficult to visualize.
To help your students visualize the relationship between the diameter and the circumference, select four cylindrical objects such as a glass, a film canister, a toilet paper roll, etc. A tennis ball canister with the three balls inside should be one of these objects. Have students number their paper 1-4 and write the name of each item. Tell them you will be having them decide which is greater, the circumference of the object or the height of the object. As you show them each object, they should write their guess for which is greater, either "circumference" or "height", next to the name of object. When they have written their guess for each object, show the length of the circumference by wrapping a measuring tape around the object. Then hold that length along the height so the students can compare the two lengths. They will be surprised when the circumference proves to be longer than the height of the object, because circumference is difficult to visualize.
Tell them estimating distance around is very difficult to do. The way you guess is to estimate the distance across the center (the diameter) and try to visualize a little more than three of those distances. That will be the distance around or the circumference. Ss you visually estimate the height of the object as compared to the circumference, you try to estimate about three diameters and compare that to the height. Tell them this relationship between the diameter and the circumference of a circle is called Pi. In any true circle the circumference will always be a little more than three diameters. Have them look at the formula on their Class Reference Sheet connecting this idea with the formula, C = πd, or C=2πr. Using the tennis ball canister is especially effective since it contains three round balls. The height should be very close to the circumference for this object.
In order to find circumference, then, we need the measure of the diameter, or of the radius. Q. Think-Team-Share: If we only know the measure of the radius, how could we know the measure of the diameter?
Movement: Use team formations where student groups stand and demonstrate circumference, diameter and radius.
Journal: Work with students to complete the Diameter, Radius, and Circumference sections of the Frayer Model for vocabulary.
Lesson Segment 2: How can I find the circumference?
Have students look at the Math 7 Class Reference Sheet and find the formula for circumference of a circle. Ask several students to read the formula saying the word indicated by the variable. For example: "Circumference equals 2 times Pi times the radius. Do Pairs Coach to have them practice finding circumference for the following using their calculators for computations. In Pairs Coach students work in pairs where one person is the coach explaining how to do the problem and the other is the scribe writing what the coach is saying to do. Students should take turns being coach and scribe for these four problems.
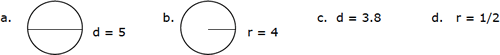
Lesson Segment 3: What information is needed for finding area of a circle?
Remind students that area is always measured in squares. Review the Perimeter, Area, Volume Song and review area being represented in square units.
Have students predict the total number of square centimeters in the whole box of the Counting The Area of a Circle worksheet (100 x 4 = 400) and write their prediction.
Q. Did anyone find a way to do this without having to literally count every little square? Discuss the idea of 10² x 4 sections.
Q. Which would have a greater number of squares, the circle inscribed in the square, or the whole box on the worksheet? Ask students to predict the number of squares in the circle and write that down. Discuss how they decided.
Q. did anyone find a faster way to estimate the number of squares in the whole circle than actually counting every single square and parts of squares? Discuss how they found the number of square units. Lead them to see they could have found the area of one of the 4 sections and then multiplied by four. The length of one of the four squares is 10. The radius of the circle is also 10. Have students highlight the length of one of the quarter boxes with colored pencil or crayon to show the length of the side of one quarter. Review the formula for area of a square ( s²). Write the formula for finding area of the large square ( 4s²). Remind them that the length of the side of one quarter of the box is also the radius of the whole circle. Write the formula for area of a circle (3.14r²). Compare this formula to the formula for finding the squares in the large box (Whole Square Area = 4s²). The whole Circle Area is less than the area of the whole box. The box has an area of 4r² while the circle's area is a little less, 3.1r².
Just like we need to know the length of a side of a square to find the area by squaring that number, we also need to know the length of the radius to find the area by squaring that number. Pi is also needed for the formula.
Have student write the answer for the questions below the box on the Counting Area of a Circle worksheet as you discuss these ideas.
Work with students to complete the Area part of the Frayer Model
Lesson Segment 4: How can I find area for a circle?
Have students find the formula for area of a circle on the Math 7 Class Reference Sheet. Review how the radius measurement can be found if the diameter is given? Use this circle for the example:
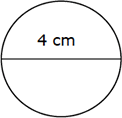
Do Mix-Freeze-Pair where students move around the room until you say freeze. The person closest to them becomes their partner. Sketch a circle on the overhead giving the radius length. Ask students to think about what the diameter would be. Then, ask the "partner with the fewest pets" to be the speaker to tell the other partner the answer and how they know. Have students mix-freeze again and sketch a second circle giving the measurement for the diameter. Ask them to think about how they would know the radius length. Ask "partner with lightest colored shoes" to be the responder.
Practice: Play Red Rover for some problems for circumference and area of a circle from an appropriate text assignment. In Red Rover, teacher gives a problem to the class. Students work the problem discussing with team. Then all teams simultaneously call a person to come to their team from the next higher numbered team. That Rover comes over to the team, sits down and explains how their team found the answer. The listening team then agrees or disagrees and discusses why. If the Rover explained correctly, the Rover's team gets a point.
Assessment Plan
Performance task, writing
Bibliography
This lesson plan created by Linda Bolin.
Updated: 02/05/2018


 UTAH EDUCATION NETWORK
UTAH EDUCATION NETWORK

 Justin
Justin Braxton
Braxton Dani
Dani Kayla
Kayla Katie
Katie Matthew
Matthew Rob
Rob Val
Val
