Math 5 - Act. 10: What's My Function?
Summary
Students will use input / output tables to help them solve algebraic equations.
Materials
Websites
- Math Solutions
- NCTM E-Standards
- Patterns in Mathematics
This site is an interactive activity where students enter in two numbers and the function is a "mystery." It is like a function machine and students can continue to try it with different numbers until they think they can solve it and then the computer tests them.
- Two of Everything by Lily Toy Hong
- Overhead calculator for teacher
- Paper and pencil
Additional Resources
Books
Lessons for Algebraic Thinking by Maryann Wickett, Katharine Kharas and Marilyn Burns
Challenge Math by Edward Zaccaro
Elementary School Mathematics by John A. Van De Walle
Beginning Algebra Thinking for Grades 3-4 and 5-6 by Shirley Hoogeboom and Judy Goodnow
Magazine
The Mailbox Intermediate April/May 2001
Video
Disney's Donald in Mathmagic Land (includes information about Fibonacci number sequences).
Background for Teachers
The numeric relationship between the frame number and the number of objects in the frame is a powerful pattern. If a rule can be discovered that can give the value of any frame in terms of the frame number, the number of objects in any frame can be determined without building or calculating all of the intermediate frames in the pattern.
These vocabulary terms should be taught and emphasized during the lesson:
Variable: a letter, symbol, or other placeholder in a mathematical expression that has an unknown value
Function: a relationship between two variables in which the value of one variable (often called the output) depends on the value of the other variable (often called the input)
Equation: a mathematical sentence that contains an equal sign
Intended Learning Outcomes
3. Reason mathematically.
4. Communicate mathematically.
Instructional Procedures
Invitation to Learn
It is a good idea to give the students plenty of experiences with input/output
tables before having them look for patterns and function relationships. One
way they could do this is to have a race.
Have students come to the board and draw an input/output T-chart with five rows. Then have each student write down the five numbers you call out on the input (left) column such as 5, 12, 18, 25, and 40. Remind students that the input is the number to which an operation rule is applied, and that the output number is the result of that operation. Next announce a rule such as "add 15" and have each player write the rule at the top of their chart. On a signal, the students fill in the output column using the rule, then turn and face the class. When both are finished have the class help you check their work. They could score one point for each correct answer and five points for whoever finishes first. Continue playing with different input numbers and different rules. This will help students feel comfortable with how these types of tables work. In addition, you could have students who are still in their seats do this activity in their math notebook at the same time as those who are doing it on the board.
Instructional Procedures
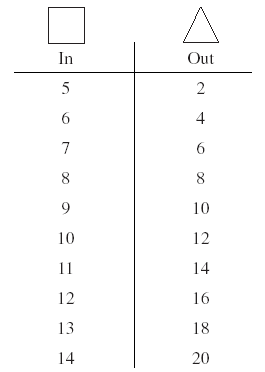
- Begin by reading Two of Everything. Make a T-chart on the board to show
what went into the pot (input value) and what came out (output value).

- Ask what would happen if you put 3 coins in the pot and write "3" midway down the In column. Students should state that 6 will come out. Continue by asking what would happen if you put in four coins, then five, ..., ten?
- Ask students to describe to you what patterns they notice in the columns.
- Ask if anyone sees a different pattern. Continue to record responses and discuss.
- Lead students to these descriptions: "The Out number is equal to the In number times two," or "The Out number is equal to the In number added to itself," or "The In plus In equals Out."
- Explain that an easier way to describe these patterns is to use symbols
(variables) in place of the words. Draw a square above the In column and a
triangle above the Out column.
- Use one of the sentence descriptions, such as "The Out number is equal
to the In number times two." Ask which symbol represents the Out number
(the triangle) and which symbol represents the In number (the square) and
write the symbolic/algebraic equation:
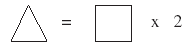
- Show the other algebraic equations:

- Now refer back to the pot and T-chart and ask the students what would happen
if the pot did something different or followed a new rule. Again make a T-chart,
enter in numbers, and conduct a discussion until students discover the new
rule (function). An example could be:

- Have students guess the next number in the pattern sequence and practice writing the algebraic equations.
- After the rule/function has been determined, see if students can skip several numbers and follow the rule for a larger number (e.g., What would the output be if the In was 30? 150, etc).
- Conclusion: Using organized lists, or tables and variables, helps solve problems and understand patterns. This is using the power of patterns to predict beyond the information currently available.
Extensions
Attachments
-
find_pattern.pdf
Find the Patterns Worksheet
Possible Extensions/Adaptations
Calculator game
Tell students that they have a "mission possible" and that they
have to figure out the mathematical mystery. But instead of you giving them
the rule and having them figure out the number answers, you are going to give
them the number answers and have them figure out the rule.
Have students prepare to write down a series of numbers and try to figure out the pattern. Using the overhead calculator and without letting the students see what you are entering, enter 2 + 5 =; let the students see the 7 then continue to press the = button several times (they will see 12, 17, 22, 27, etc.).
When several students believe they have figured out the pattern rule allow them to share. You can also have them observe the number in the ones place. How long is it before the pattern begins to repeat? Do this activity several times with different beginning arithmetic problems.
Homework and Family Connections
You could use the Find the Patterns worksheet for homework. Have students make
the tables, find the patterns, write the equations, and answer the questions
for each.
Students could also do the extension activity at home and create In/Out charts with their own rules and fill in several examples on the chart.
Assessment Plan
Allow the students to work in pairs to choose a rule, write it as an equation, and generate a T-chart. Brainstorming a list of possible rules might be helpful so that students who have difficulty deciding on a rule of their own or who want to make their rules too complicated have some guidelines to follow.
Updated: 02/05/2018


 UTAH EDUCATION NETWORK
UTAH EDUCATION NETWORK

 Justin
Justin Braxton
Braxton Dani
Dani Kayla
Kayla Katie
Katie Matthew
Matthew Rob
Rob Val
Val
