Prime and Composite

Summary

Students will use manipulatives to learn about composite and prime numbers.

Materials

For class:

• We are Prime/ Composite Numbers posters
• Sieve (or picture of a sieve)

For each student:

• Graph paper
• Manipulative Master or manipulatives
• Sieve of Eratosthenes worksheet
• Prove or Disprove worksheet
• Colored pencils

Additional Resources

Book

• Mathland, Journey Through Mathematics: Student Resource Book Grade 6, by Nancy Homan; ISBN 0762212411

Background for Teachers

Students learned to classify whole numbers from 2 to 20 as composite or prime, and 0 and 1 as neither prime nor composite, in fifth grade.

Every whole number greater than 1 is either a prime or composite number. A prime number has exactly two factors, 1 and itself. A composite number has more than two factors.

Commutative property is the fact that changing the order of addends or factors does not change the sum or product (e.g., 4 x 7 = 28 and 7 x 4 = 28).

Rules of divisibility

• A whole number is divisible by 2 if and only if the ones digit is even.
• A whole number is divisible by 3 if and only if the sum of its digits is divisible by 3.
• A whole number is divisible by 5 if and only if the ones digit is 5 or 0.
• A whole number is divisible by 6 if and only if it is divisible by 2 and 3.
• A whole number is divisible by 9 if and only if the sum of its digits are divisible by 9 (or 3).
• A whole number is divisible by 10 if and only if the ones digit is 0.

Intended Learning Outcomes

1. Demonstrate a positive learning attitude toward mathematics.
2. Become mathematical problem solvers.
3. Reason mathematically.

Instructional Procedures

Invitation to Learn
Pass out 12 centimeter cubes to each student. Have students make different shapes with the cubes. Share examples and point out examples and nonexamples of arrays. Write a definition of "array" as a class.

Instructional Procedures

Day 1

1. Use the Manipulative Master to create an array for numbers from 3 to 20. For example, say to the class, "Using your manipulatives, show me what 4 looks like. How many ways can you make a complete rectangle using only four squares?"
2. Continue through all numbers, 3-20.
3. Transfer arrays onto graph paper and label each rectangle.
   Example:
   
4. Circle each factor using one color. Put a circle around each product using a different color.
   Example:
   
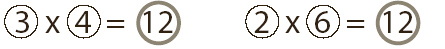
5. Point out the commutative property--the fact that changing the order of addends or factors does not change the sum or product.
   Example:
   3 x 4 = 12 and 4 x 3 = 12
   factors 1, 2, 3, 4, 6, 12
6. Connect two factors using a curved line that resembles a rainbow. Draw a square around numbers that are the square root.
   
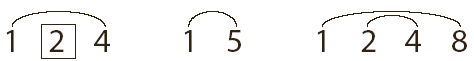
7. Numbers with exactly 2 factors are prime numbers.
8. Numbers with more than two factors are composite numbers.
9. The numbers 0 and 1 are neither prime nor composite. 1 is a unique counting number. 0 is not a counting number.

Day 2

1. Before class, place the We Are Prime (Composite) Numbers posters in different corners of the room.
2. Before class, prepare a sheet of graph paper for each student in your class by writing a different number at the top of each sheet. Begin with the number two and continue in order until you have enough for each student (e.g., If you have 36 students in your class, you would use the numbers 2-27 for this activity.).
3. Pass out a sheet to each student. Instruct students to complete their sheets as follows:
   • Draw all of the possible arrays for the number.
   • Label the length and width of each array.
   • Write multiplication sentences for each array and circle factors in red and products in blue.
   • Draw a factor rainbow for the number.
4. As the students finish, begin sending them to different corners of the room depending on whether they have a prime or composite number. Have the students take their completed papers with them.
5. Have the students in each corner compare their numbers with other members of their group and look for things that their numbers have in common. If the students are having a difficult time seeing similarities, prompt them to look at the number of factors and arrays. Discuss the findings as a class.
6. Have one member of each group hold up the We Are Prime (Composite) Numbers posters.
7. Have students return to their seats and write definitions of prime and composite numbers in math journals.
8. Gather papers from students and randomly pass them out again. After looking at their new number, have students move to the correct corner of the room again. Continue to do this until all students can correctly move it either the prime or composite corners of the room.
9. If you have been hanging the Number Posters up around your classroom, draw students' attention to them at this time. Look at the posters and discuss how the number one is different than the other numbers. Write a definition for unique number in math journals.

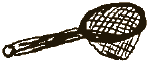Day 3

1. Show a sieve. What is it? What is it used for? How does it work?
2. We can sort numbers just like a sieve separates and sorts material.
3. Using the Sieve of Eratosthenes, complete the hundreds chart as follows:
   1. As a class, cross out the 1 on the chart.
   2. Putting your finger on 2 count by twos and color the top left corner of each number square yellow.
      Teacher Note: As students begin coloring, they will most likely begin to see a pattern. Explain the rule of divisibility for 2--A whole number is divisible by 2 if the ones digit is even.
   3. Put your finger on 3. Counting by threes color in the top right corner of each number square orange.
      Teacher Note: As students begin coloring, they will most likely begin to see a pattern. Explain the rule of divisibility for 3--A whole number is divisible by 3 if the sum of its digits is divisible by 3.
   4. Place centimeter cubes on all multiples of 6. Discuss patterns and divisibility for 6.
   5. Put your finger on 5. Count by fives and color the bottom left corner of each number square green.
      Teacher Note: As students begin coloring, they will most likely begin to see a pattern. Explain the rules of divisibility for 5 and 10--A whole number is divisible by 5 if the ones digit is 5 or 0. A whole number is divisible by 10 if the ones digit is 0.
   6. Put your finger on number 7. Count by sevens and color the bottom right corner of each number square blue.
   7. The boxes with nothing colored are prime numbers. Color these boxes red.

Day 4

1. How can you tell people apart? How can you tell people apart when you cannot see them? (fingerprint)
2. Just like every person has a unique fingerprint, each number has a unique "factorprint." This factorprint is the number's prime factorization. It is the set of prime numbers whose product equals the number.
   Factor Trees
   

Birthday Cake
Start with lowest prime number (2).
If 2 will not work, move to 3, etc...

Extensions

• Have students work in pairs or small groups to develop divisibility rules. Discuss as a class and complete rules as listed in the Background for Teachers section.
• Prove or Disprove worksheet.
• Have students research Eratosthenes and tie to a Social Studies unit on Greece.

Family Connections
Students explain the Sieve of Eratosthenes to a family member.

Assessment Plan

• Observation of students, class discussion, and discovery.
• The Prove or Disprove worksheet may be used as an assessment tool.

Bibliography

Research Basis

Hatfield, M., Edwards, N., Bitter, G. & Morrow, J. (2000). Mathematics Methods for Elementary and Middle School Teachers. New York, New York. John Wiley & Sons Inc.

"An activity-based approach to teaching with an emphasis on using manipulatives to build conceptual understanding! This valuable book combines practical teaching ideas, video examples, updated assessment techniques, and the NCTM Assessment Standards to give teachers all the background they need to introduce elementary and middle school students to the wonders of mathematics. Provides training and practicing teachers of kindergarten to the eight grade with ideas, techniques, and approaches to teaching mathematics such that their students will be prepared for later study."